Bifid

History

The Bifid cipher was invented by the French amateur cryptographer Félix Delastelle in the late 19th century. Delastelle was known for his contributions to various cryptographic systems, including polygraphic ciphers.

The Bifid cipher was introduced by Delastelle in 1895 as a method to improve the security of classical ciphers such as the simple substitution cipher. It is a polygraphic substitution cipher that combines transposition and substitution techniques.

Delastelle's inspiration for the Bifid cipher came from an earlier cipher called the Trifid cipher, which used a 3x3 grid. Delastelle expanded the concept by creating a 5x5 grid for the Bifid cipher. The grid contains all the letters of the alphabet (excluding J) arranged in a square, with each letter associated with its row and column indices.

The Bifid cipher encrypts the plaintext by first converting letters to their corresponding row and column indices in the grid. These indices are then combined into pairs, and the resulting coordinates are used to derive the ciphertext. Decryption involves reversing the process to obtain the original plaintext.

The Bifid cipher gained popularity and was widely used during the late 19th and early 20th centuries. It was employed by individuals, organizations, and military groups to secure sensitive information. However, with the development of more advanced encryption techniques, the Bifid cipher gradually lost its significance and is now primarily studied as a historical example of a polygraphic substitution cipher.

Some quotes from online:

“In classical cryptography, the bifid cipher is a cipher which combines the Polybius square with transposition and uses fractionation to achieve diffusion. It was invented around 1901 by Felix Delastelle”.

“The Bifid cipher was invented by the French amateur cryptographer Félix Delastelle around 1901. It is a fractionating transposition cipher, and was considered as a system of importance in cryptology. The Bifid cipher uses a Polybius square to achieve the fractionation. Each character depends on two plaintext characters, so it is a digraphic cipher”.

How it works

Bifid ciphers are a more complicated version of a Polybius cipher, in that where a Polybius cipher encrypts letters (plaintext) into numbers (cyphertext), a bifid cipher has an added step of converting these numbers into completely different letters from the plaintext. Looking at the plaintext “pilgrims” as an example, the encryption starts by first converting each letter into a pair of numbers, which are the ‘row’ and ‘column’ of where the letters appear in the grid below:

As we can see from the grid, the position of the letter ‘p’ is ‘3 5’, ‘i’ is ‘2 4’, ‘l’ is ‘3 1’, etc. The conversion from the plaintext “pilgrims” into numbers can be written out as two rows and N columns (N is number of letters in the plaintext), such that the ‘row’ number of each letter is written in the top row and the ‘columns’ number of each letter is written in the bottom row. The plaintext “pilgrims” appears like this:

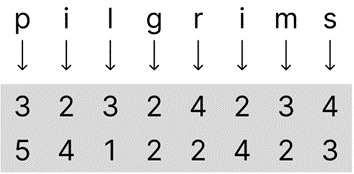
By reading each pair of numbers ‘vertically’, ‘p’ is ‘3 5’ as its supposed to be. The next step is to convert these numbers into a new word, which involves splitting out these numbers into new/different pairs of numbers. The picture above pairs numbers ‘vertically’, so now the numbers will be paired ‘horizontally’, as shown below:

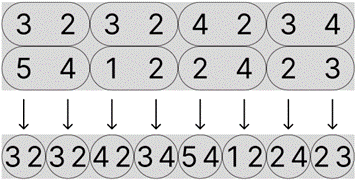
Here the ‘horizontal’ pairs have been highlighted, so we get ‘3 2’ which is the 3^rd row and 2^nd column of the grid (which is ‘M’) and so on. The arrows in the picture above indicate a transition from a 2xN grey box to a 1xN grey box, which can be more convenient for writing out the letters that these pairs of numbers lead to. This is shown below:

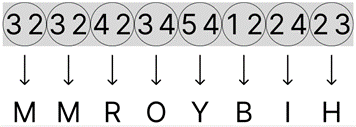
Thus when converting from numbers into letters, we get the cyphertext “MMROYBIH”. Based on the pictures above, using a bifid cipher is a 3-step process, or 2-step process if you don’t change the grey box from 2xN to 1xN.

In order to decipher a bifid cipher, do the same 3-step process for encryption but in reverse. To save time, all the steps will be shown in the picture below:

The first step (in red) is to convert the letters in the cyphertext “MMROYBIH” into ('horizontally') paired numbers. The second step (in blue) is to change the grey box from 1xN to 2xN, showing the switch from ‘horizontally’ paired numbers to ‘vertically’ paired numbers. The third and last step (in yellow) is to convert the paired numbers into letters, giving the plaintext “pilgrims”.

Please note that the length of the plaintext and cyphertext are the same and the game will have between a 3-letter and  8-letter plaintext/cyphertext. The 2xN grey box will change width depending on the length of the plaintext/cyphertext. Also note that a plaintext/cyphertext with an odd number of letters results in a 2xN grey box with an odd number of numbers in each row. Take the 3 letter cyphertext “DRX”, as shown in the picture below:

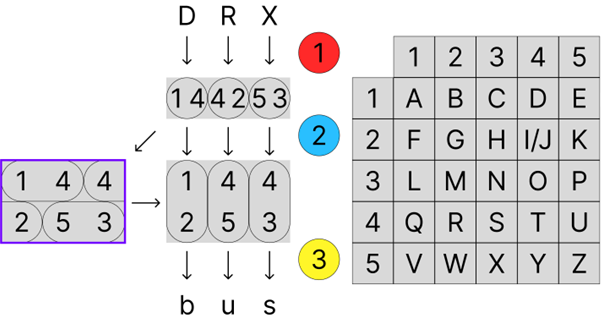
We see that the 2x3 grey box (highlighted in purple) shows the ‘horizontally’ paired numbers, where the second pairing ‘4 2’ starts at the end of row 1 and finishes at front of row 2. This is just something to keep in mind, since the game will automatically place the ‘horizontally’ paired numbers into a 2xN grey box and the user simply has to read the numbers as ‘vertically’ paired numbers.

How it works (in the game)

The game will present a cyphertext (of letters) and ask for the plaintext. A grid will be provided as an interactable tool, alongside a 2xN grey box underneath the grid.

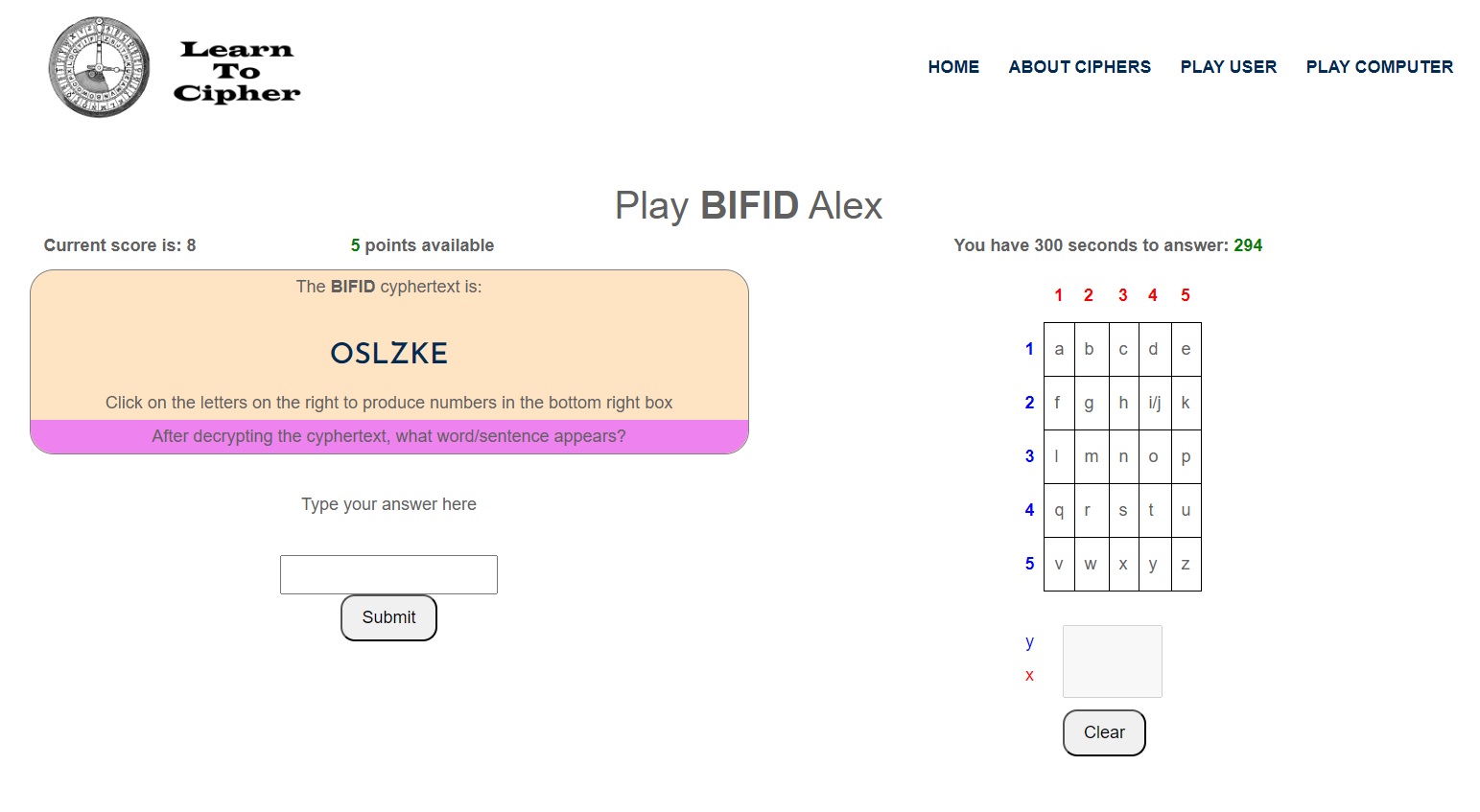
The user can interact with the grid by clicking on a letter, which places the paired numbers of that letter ’horizontally’ into the 2xN grey box.

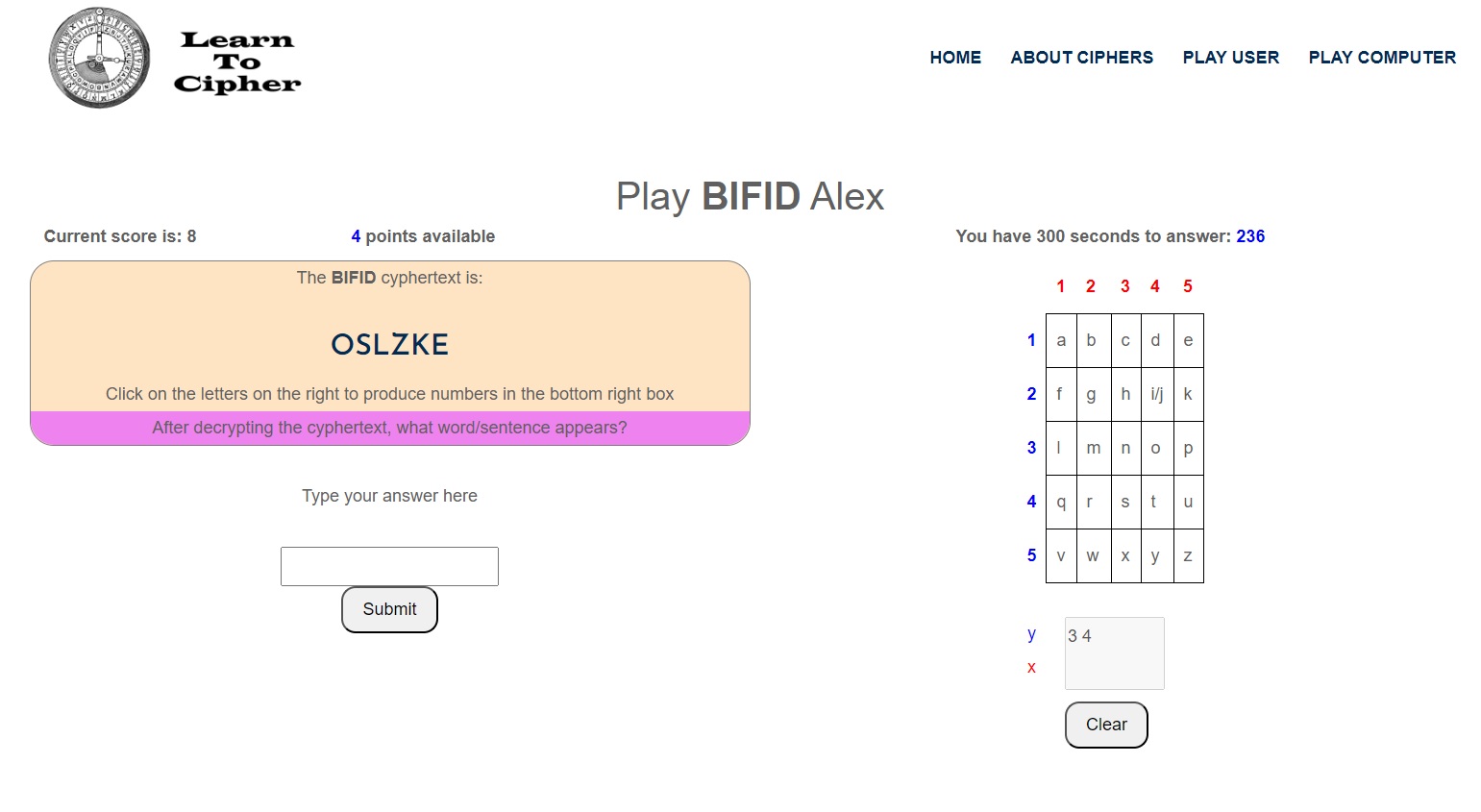
Here the first letter ‘O’ has been clicked on the grid and it’s position ‘3 4’ has been placed into the grid as ‘horizontally’ paired numbers.

The idea is for the user to click each letter in the cyphertext, thus creating a 2xN grey box with the ‘horizontally’ paired numbers and once the grey box is filled the paired numbers can then be read ‘vertically’ to find the plaintext.

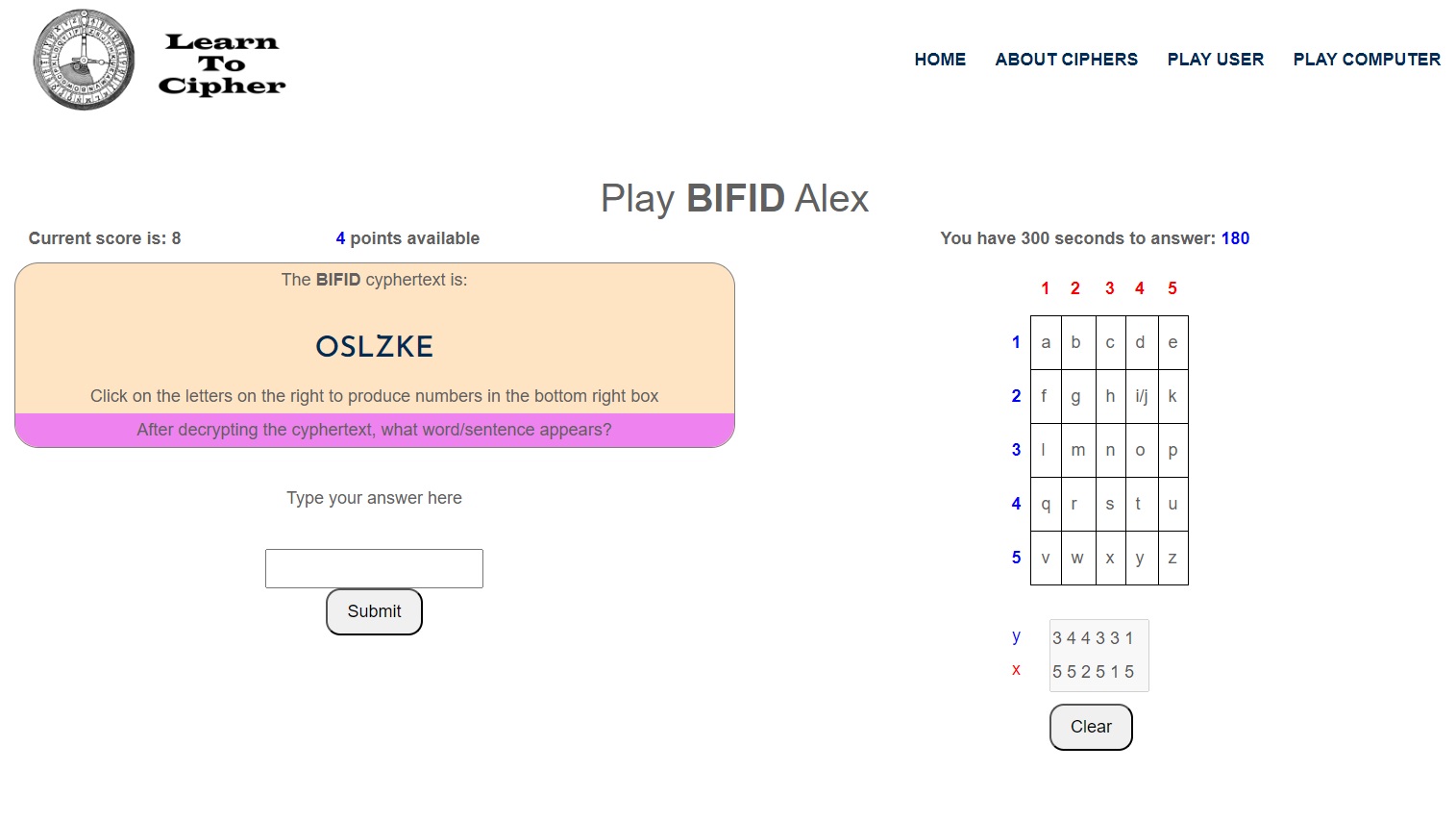
The grey box will change width depending on the number of letters in each cyphertext/plaintext (minimum 3 letters, maximum 8 letters).

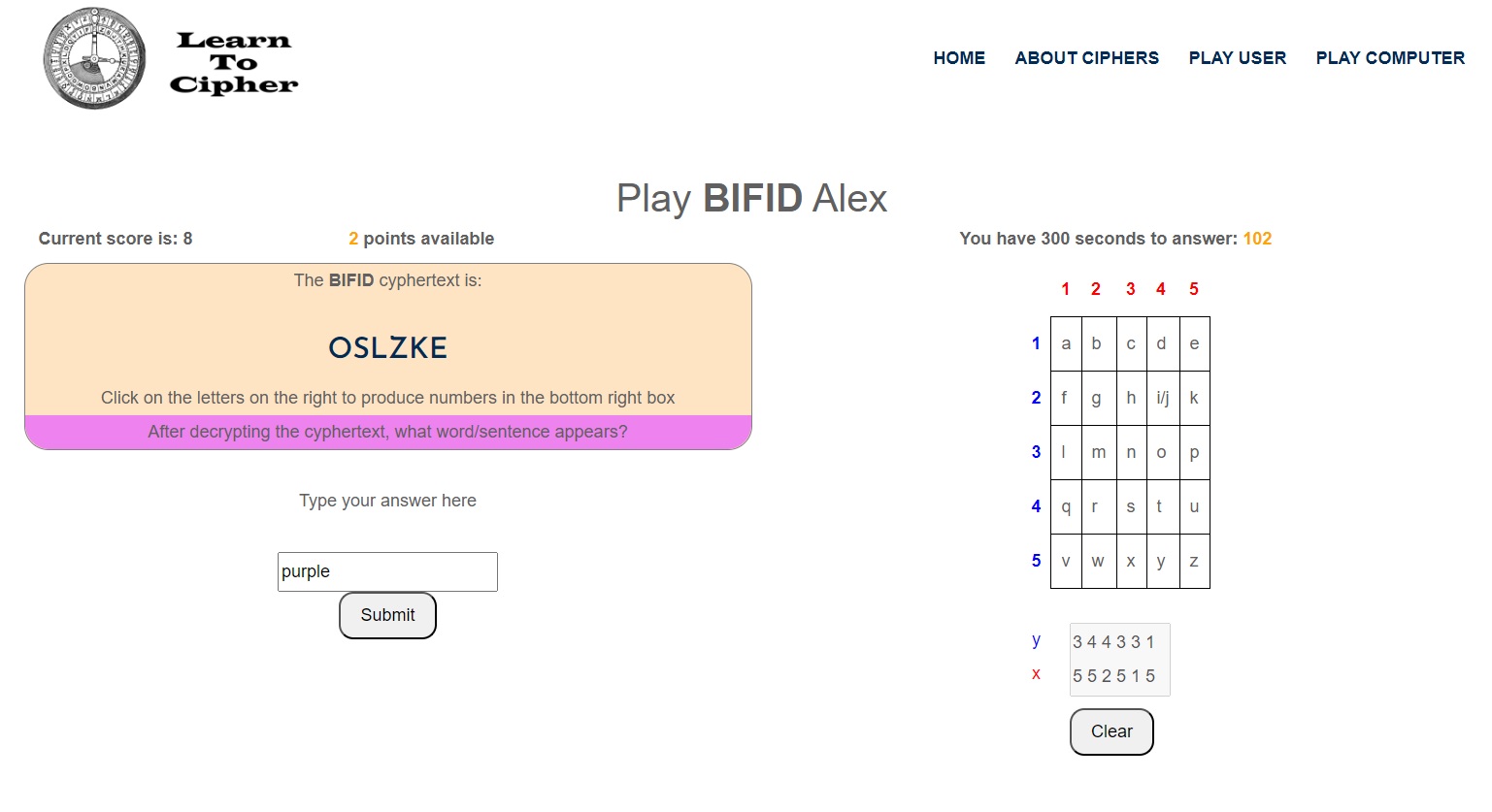
Once the 2xN grey box is full, the user then reads the ‘vertically’ paired numbers and types in the plaintext into the answer box, which in the example the plaintext is "purple".